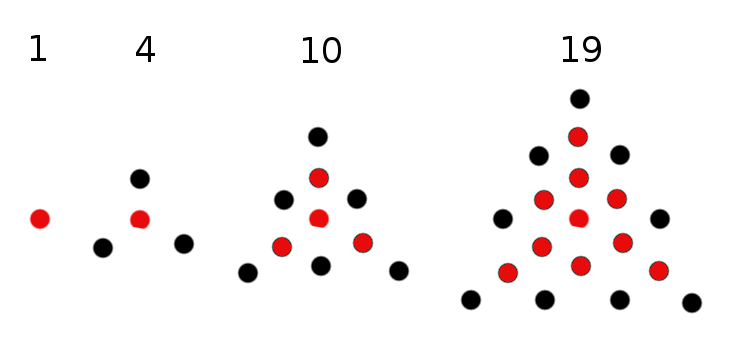
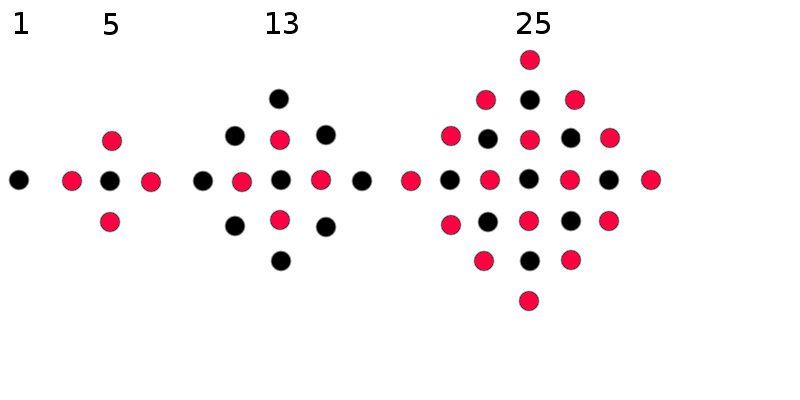
Tutti i Levanesi sono castani
Ma sarà vero?
Sono stato molte volte a Levane, un paesone del Valdarno superiore sud situato tra Arezzo e Firenze, lungo la Statale 69 del Valdarno. Non ci avevo fatto caso, ma poi mi hanno fatto notare che tutti i Levanesi (gli abitanti di Levane) sono castani. Oh sembra sia proprio vero, ogni volta che vedo un levanese, questi ha i capelli castani, immancabilmente, quindi, induttivamente, mi viene naturale affermare che tutti i Levanesi sono castani.
Personalmente sono portato verso il pensiero scientifico, logico o matematico, purché sostenuto da prove chiare.
Certo per essere sicuro che tutti i levanesi sono castani dovrei incontrarli uno ad uno e verificare, troppo difficile anche appostandomi al bar o all’incrocio.
Tutti
Potrei, più comodamente, usare la logica, usando altre prove. Se è vero che tutti i levanesi sono castani deve essere vero anche il suo contrario logico. Cioè che tutti i non Levanesi sono non castani. Infatti, io che sono di Bucine, sono moro. Cioè io non Levanese sono non castano. Conosco anche uno di Montevarchi biondo, altra prova a sostegno della tesi induttiva che siccome un Montevarchino è biondo un non levanese è non Castano quindi tutti i Levanesi sono castani.
Non farebbe una piega, se non avessi incontrato uno di Laterina con una bella chioma castana, allora se un non Levanese è castano almeno un Levanese è non castano.
Ma perché ho sbagliato così clamorosamente le mie conclusioni? Il processo di induzione, derivare regole generali da una singola prova è un metodo usato da tutti, ogni giorno, per stabilire cosa fare. Se al mattino scendiamo dal letto e poggiamo i piedi nel pavimento senza sprofondare al piano inferiore. Significa che ci aspettiamo, correttamente, che ogni mattina successiva possiamo alzarci nello stesso modo senza preoccuparci della presenza o solidità del pavimento.
Ragioniamoci bene
Beh, a volte il nostro ragionamento è troppo affrettato e ci fidiamo troppo delle poche prove che il metodo induttivo ci da. Infatti non basta che si rompa l’auto partendo il martedì mattina per le vacanze, per confermare il detto che “Di Venere e di Marte, ne si torna ne si parte”.
Comunque senza il metodo induttivo molte cose non riusciremmo a farle. Infatti dopo un primo insuccesso generalizzeremo che l’azione connessa è impossibile o pericolosa. Meglio non farla. Allora conviene sempre valutare quanto sia probabile che un accadimento si ripeta. Se valuteremo bene, come quasi tutte le persone sono in grado di fare le nostre previsioni saranno mediamente corrette e non avremo problemi.
Ma se il Montevarchino è biondo significa che tutti i non Montevarchini sono non biondi? Il fatto che tutti i non Levanesi siano non castani ne è un conferma, una plateale conferma direi?
Voi che ne pensate?
Giancarlo













 Proclo
Proclo
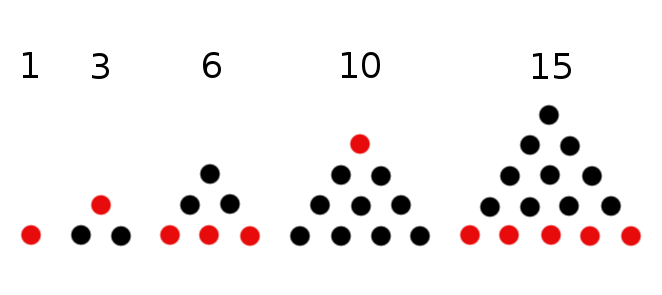

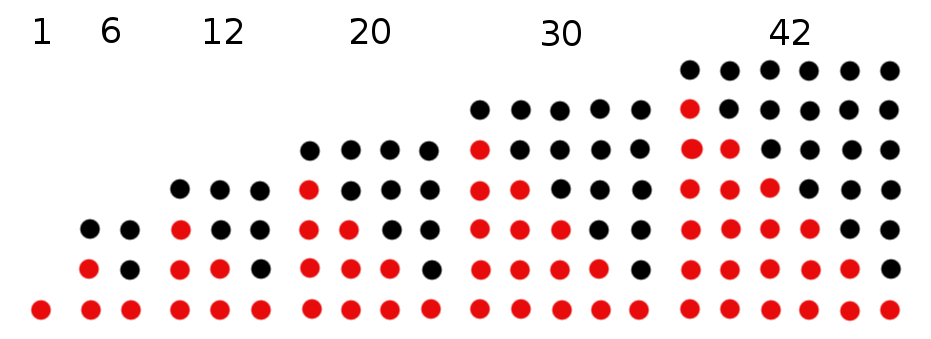
 ; questa proprietà fu scoperta da Gauss nel 1796, ed è un caso particolare del
; questa proprietà fu scoperta da Gauss nel 1796, ed è un caso particolare del  numeri triangolari è pari all’n-esimo
numeri triangolari è pari all’n-esimo  ; ogni altro numero triangolare è un
; ogni altro numero triangolare è un  Questo risultato è noto sotto il nome di
Questo risultato è noto sotto il nome di