Archivi tag: Fibonacci

Cultura,Matematica,Senza categoria

I primi numeri di Fibonacci.

Lascia un commento

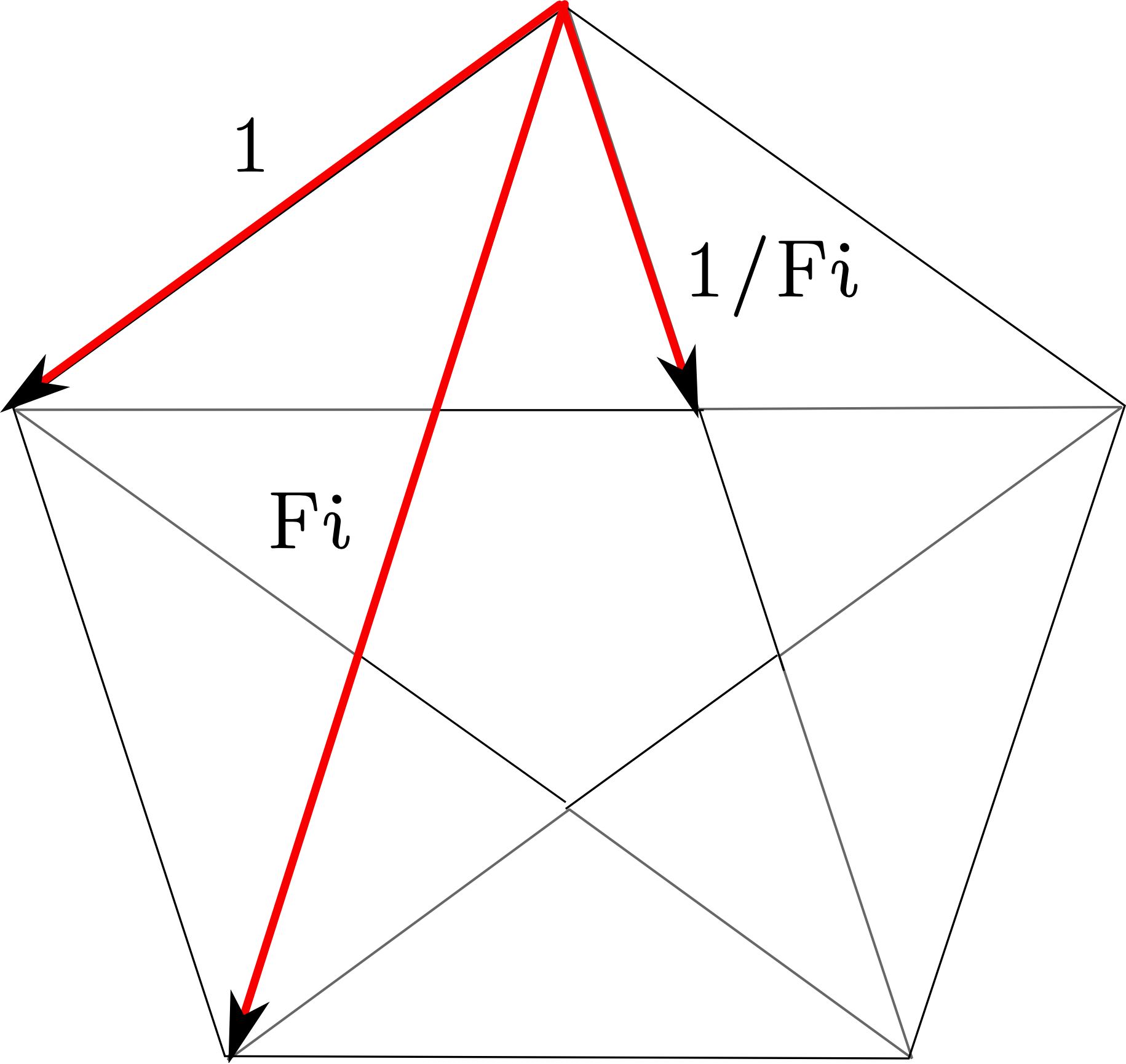
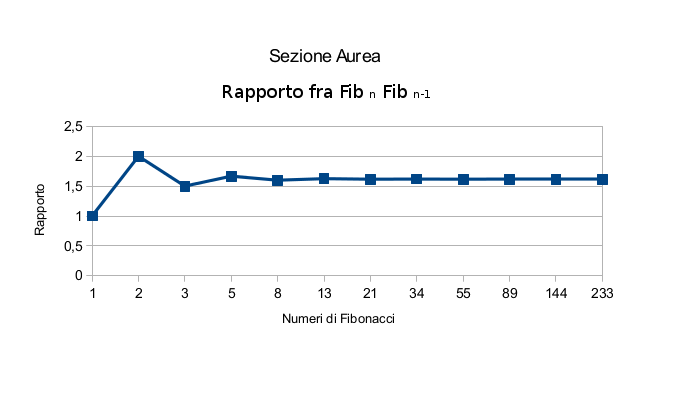
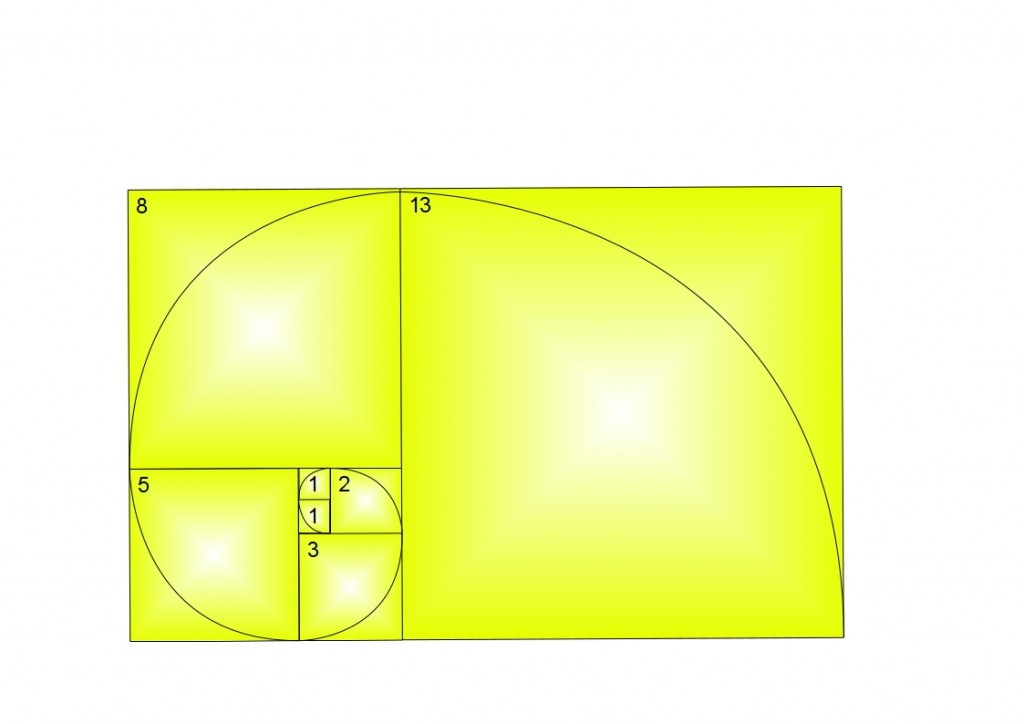
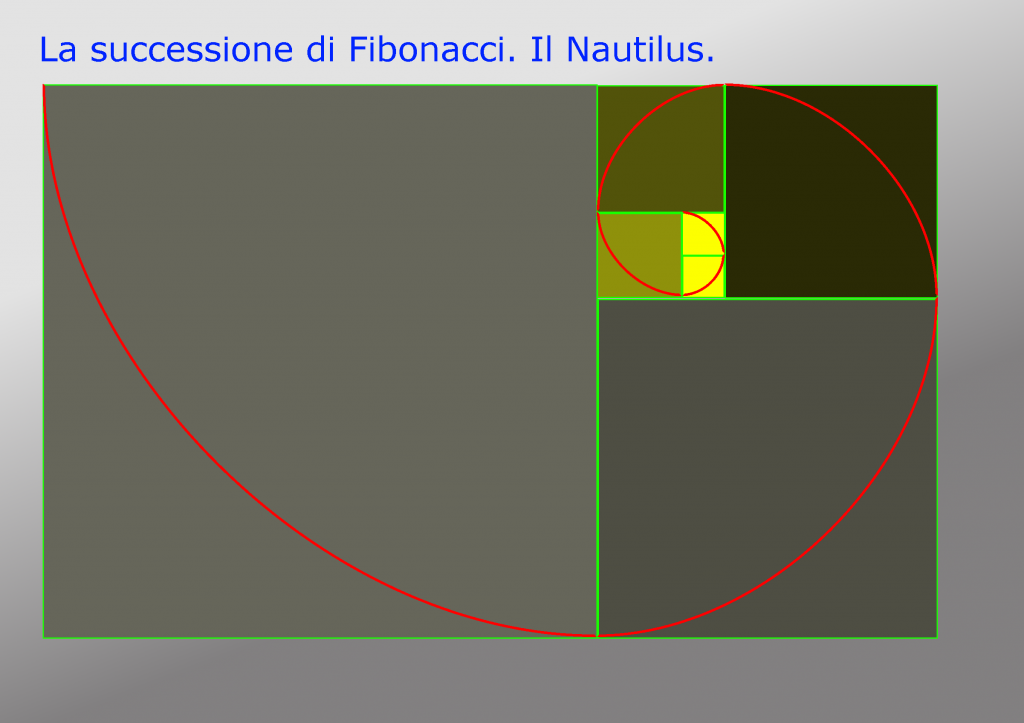
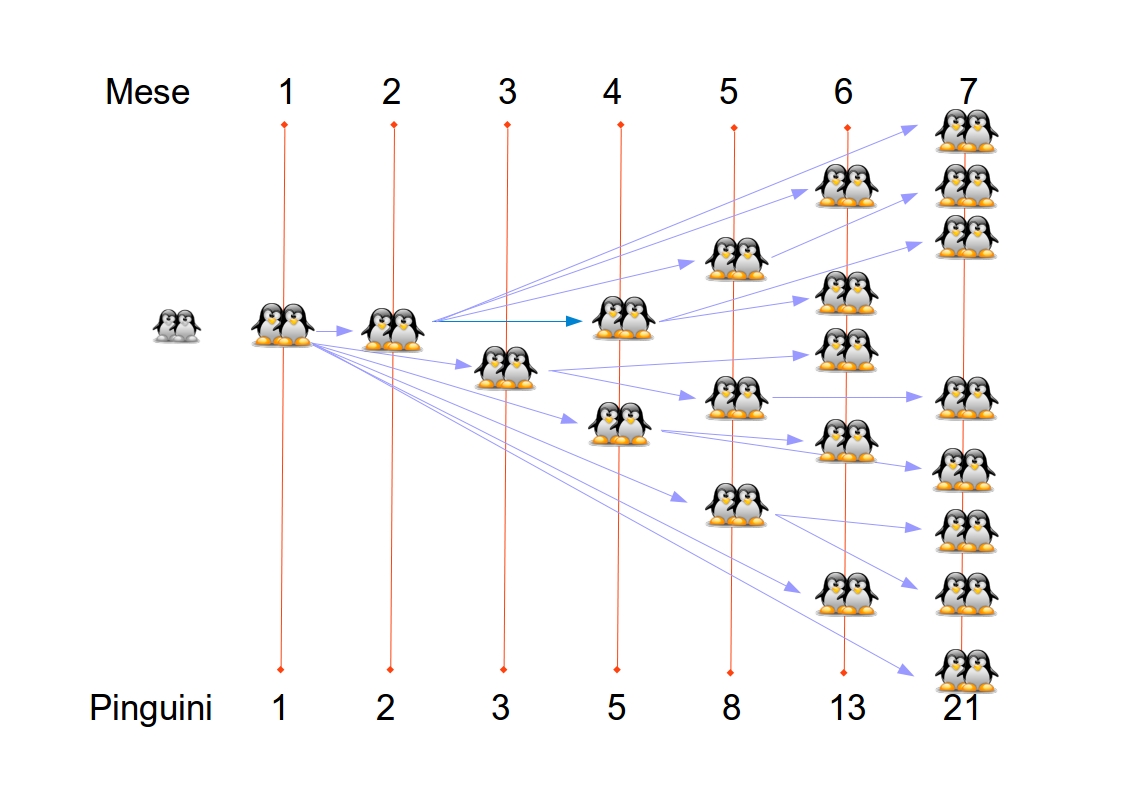
I primi numeri di Fibonacci sono:

1,1,2,3,5,8,13,21,34,55,89,144, 233,377,610, 987, 1597…

Tutti i numeri, diversi dal numero 1, possono essere scomposti in fattori primi; cioè possono essere ottenuti moltiplicando una combinazione unica di fattori primi, ovvero, può cambiare solo l’ordine dei fattori ma non il numero ed il valore dei fattori stessi. Ogni numero della sequenza di Fibonacci ha almeno un fattore diverso da qualsiasi fattore di un numero di Fibonacci precedente.

1- I numeri primi sono quelli che possono essere divisi solo per 1 e per se stessi senza ottenere resti. Ma 1, in realtà non è un  numero primo, infatti porremmo moltiplicarlo e dividerlo un numero di volte a piacere ed ottenere sempre 1, ottenendo una fattorizzazione variabile, che non garba, ne è elegante, insomma non va bene. Quindi il numero 1 sarebbe facile da scomporre  in 1×1, ma 1 non è un  numero primo, anche se un tempo era considerato il primo dei numeri primi.

2 – è in realtà il primo numero primo, perché a parte che per 1, per il quale tutti i numeri sono divisibili una o più volte, è divisibile solo per 2. E’, per me, interessante notare che questo numero primo, il primo, è anche l’unico numero primo pari. Tutti gli altri pari saranno infatti divisibili almeno per 1, per 2  e per se stessi. (I numeri primi appartenenti alla serie di Fibonacci li scriverò in Rosso).

3 – il quarto della serie, è divisibile per 1 e per se stesso, ed è, anche lui, un numero primo.

5 – è primo e ovviamente, unico e non ancora incontrato tra i divisori dei numeri della successione.

I primi numeri di Fibonacci
http://commons.wikimedia.org/wiki/File%3APascalFibonacci.svg

Ancora su i primi numeri di Fibonacci:

Adesso incontriamo la prima anomalia, il sesto numero di Fibonacci, così come il 12esimo e nessun altro, non ha(nno) almeno un fattore diverso da quelli di un precedente numero di Fibonacci.

8=2x2x2

13 – Numero primo.

21=3x7

Siamo arrivati al settimo numero di Fibonacci. Si può scomporre in una sequenza unica di fattori, di cui almeno uno unico,  cioè non ancora comparso tra quelli dei numeri di Fibonacci precedenti, il 7. (I fattori che non dividono numeri di Fibonacci precendenti li scriverò in azzurro)

34=2x17

55=5x11

89

ed ecco l’altro numero anomalo.

134=24×32

poi, fino all’infinito.

233

377 = 13 x 29
610 = 2 x 5 x 61
987 = 3 x 7 x 47
1597
2584 = 23 x 17 x 19
4181 = 37 x 113
6765 = 3 x 5 x 11 x 41
10946 = 2 x 13 x 421
17711 = 89 x 199
28657
46368 = 25 x 32 x 7 x 23
75025 = 52 x 3001
121393 = 233 x 521
196418 = 2 x 17 x 53 x 109
317811 = 3 x 13 x 29 x 281
514229
832040 = 23 x 5 x 11 x 31 x 61

Questi sono solo i primi numeri di Fibonacci, solo i primi trenta, ma va avanti così per sempre.

Da notare quanti numeri primi si incontrino nella sequenza di Fibonacci, questo la rende molto interessante.

Giancarlo

Arte,Matematica,Senza categoria,Toscana

La sezione Aurea

Lascia un commento

La sezione Aurea

Se andiamo a spulciare la successione di Fibonacci si scoprono cose interessanti. La sezione Aurea è una di queste. Se calcoliamo il rapporto fra numeri successivi della sequenza di Fibonacci Fib (n + 1) / Fib (n) notiamo un curioso comportamento: il rapporto oscilla tra due numeri molto vicini ma non diviene mai uguale.

1/1 1
2/1 2
3/2 1,5
5/3 1,6666666667
8/5 1,6000000000
13/8 1,6250000000
21/13 1,6153846154
34/21 1,6190476190
55/34 1,6176470588
89/55 1,6181818182
144/89 1,6179775281
233/144 1,6180555556

GraficamenteFibonacci sezione Aurea Dato che i numeri di Fibonacci sono infiniti il loro rapporto sarà anch’esso infinito. Per un numero di Fibonacci che tende all’infinito potremo trovare un valore limite, che indicheremo come fanno i matematici con Φ (Fi).

Detto in altro modo possiamo calcolare Φ come il limite per n che tende all’infinito del rapporto fra Fib (n + 1) e Fib (n) (dove Fib (n) è l’ennesimo numero di Fibonacci).

Matematicamente

si può dimostrare che il valore di Φ è uguale a 1 sommato alla radice quadrata di 5, il tutto diviso per 2, che da un valore numerico di circa 1,618. Una semplice dimostrazione è la lettura del grafico e relativi valori calcolati in un foglio di calcolo di libre office (calc) riportati più sopra.

Ma volendo andar a vedere la formula matematica possiamo scrivere: Fib (n + 1) / Fib (n), ma Fib (n+1) (il prossimo numero della sequenza) per definizione è uguale alla somma dei due numeri precedenti, cioè Fib (n) (il numero attuale) + Fib (n -1) (quello precedente) quindi Fib (n +1) / Fib (n) = Fib (n) + Fib (n – 1) / Fib (n) che è uguale a 1 + Fib (n – 1) / Fib (n) allora Fib (n + 1) / Fib (n) = 1 + Fib (n – 1) / Fib (n)

Per numeri n molto grandi Fib (n + 1) / Fib (n) ≈ Φ e Fib (n – 1) / Fib (n) ≈ 1 / Φ. Quindi, dopo tanto ragionamento, possiamo trasformare l’equazione precedente in Φ = 1 / Φ + 1.

Semplifichiamo moltiplicando entrambi i termini per Φ Φ x Φ=1 + Φ uguagliando a zero Φ² – Φ – 1 = 0 è un’equazione di secondo grado come aX² + bX + c = 0 che normalmente si risolve X= -b² ± √b²-4ac.

Ovvero, nel nostro caso Φ = (1 ± √1+4) / 2 la cui soluzione positiva è (la negativa non ci serve) Φ = (1 + √5) / 2 ≈ 1,618 la sezione Aurea. Dalla formula Φ = 1 / Φ + 1 si ricava facilmente l’inverso di Φ 1 / Φ = Φ – 1 ≈ 1,618 – 1 ≈ 0,618.
Quest’ultimo valore è noto anche nell’arte e nell’architettura perché consente, di ottenere figure ben proporzionate.

sezione aurea Fi

Giancarlo

Matematica,Natura,Senza categoria

Il Nautilus

Lascia un commento

Il Nautilus (di Fibonacci).

Il Nautilus, vedi wikipedia, oltre ad essere il file manager dell’ambiente desktop GNOME proprio di qualche distribuzione GNU/LINUX e il sommergibile di Verne, è anche una mollusco dotato di una splendida conchiglia che cresce con lui.

Nautilus
Nautilus sezionato.
Da Wikimedia http://commons.wikimedia.org/wiki/File%3ANautilus-seccionado-2.jpg
Nautilus
Nautilus Pompilius
Wikimedia http://commons.wikimedia.org/wiki/File%3ANautilus_pompilius_3.jpg

Ma perché parliamo di file manager e molluschi. Beh di file manager perché Nautilus era il logico proseguo della shell usata da GNU/Linux e tutti i sistemi UNIX, conchiglia dopo conchiglia si arriva al pinguino. Ma qui non c’entra nulla, qui parliamo di matematica.

LEONARDO PISANO detto FIBONACCI

Vi dice niente questo nome?

non lo ripeto, se non lo sapete guardate il primo o il secondo articolo in merito.

Vediamo di iniziare a comprendere la grandezza della successione scoperta dal Pisano.

Il Nautilus costruisce la sua conchiglia in forma di spirale logaritmica (naturalmente la forma reale è più complessa e tridimensionale ma noi la possiamo rappresentare bene in due dimensioni, disegnando appunto una spirale logaritmica.

Si vede

bene nella prima immagine del Nautilus sezionato, ora vi mostro lo schema che ho disegnato io.

il nautilus

Si vede subito che dentro ci sono i primi numeri della sequenza di Fibonacci e l’area dove sono scritti non ne è che il quadrato, cioè la spirale inizia con due quadrati di lato unitario affiancati, questi idealmente costruiscono un rettangolo di 2×1 (due quadrati di 1 affiancati) e sul suo lato maggiore.

Possiamo ora affiancare un quadrato di 2×2 (2 al quadrato, il cui lato è dato dalla somma dei due numeri precedenti). Il tutto, preso assieme, forma un rettangolo 3×2, quindi sul lato maggiore accostiamo un quadrato 3×3 (3 al quadrato con lato uguale alla somma dei due numeri precedenti), se continuiamo a costruire un nuovo quadrato sul lato maggiore (5) avremo un rettangolo simile al precedente ma di dimensioni maggiori (5×8). Possiamo continuare così all’infinito, 8×13, 13×21, 21×34,… la somma dei due lati affiancati degli ultimi quadrati ci darà il lato del nuovo quadrato ed incrementerà la successione di Fibonacci:

1,1,2,3,5,8,13,21,34,…

Se ora facciamo passare una curva tra i due angoli opposti di ogni quadrato, avendo cura di far coincidere il secondo angolo di un quadrato con un altro del secondo del quadrato adiacente e piegando la curva verso quello opposto, costruiremo la nostra spirale, che crescerà indefinitamente, sempre nello stesso modo, sempre seguendo la successione di Fibonacci.

Nautilus

Per quanto riguarda il Nautilus, la sua conchiglia crescendo secondo questa successione permette di creare spazi interni sempre maggiori, adatti a contenere il corpo del mollusco che si espande, crescendo, nella stessa maniera.

Curiosamente

la spirale parte con due quadrati uguali, i due numeri unitari, ma se invece del primo quadrato di lato 1 avessimo un quadrato di lato dimezzato, cui accanto trova posto un quadrato di lato un quarto e così via, la spirale continuerebbe in senso inverso? Ovvero partirebbe prima? Con la stessa forma? Si raggiungerebbe mai il centro? lo zero. Mi sa che siamo al limite.

Che spettacolo,

che spettacolo la natura,

e che spettacolo anche la matematica,

ma sui numeri della successione c’è altro da dire, molto altro,

e

noi lo diremo,

dopo,

arrivederci.

Giancarlo

Matematica,Senza categoria

Fibonacci, la successione.

Lascia un commento

La successione di Fibonacci visuale.

La successione di Fibonacci, di cui ho parlato in un altro articolo, si può anche rendere per immagini.

Al posto dei conigli il Pinguino TUX.

Pinguini di Fibonacci
Non ho usato la solita grafica dei conigli, perché i pinguini sono molto più belli, poi questa dovrebbe rendere meglio la riproduzione e le varie generazioni. La coppia piccola e in B/N all’inizio rappresenta la prima coppia che non diviene fertile che al primo mese. Fibonacci comunque usava partire da una coppia già adulta che si riproduceva già nel primo mese, per riportarsi nelle sue condizioni i numeri delle colonne dei mesi vanno sottratti di una unità, cioè si conta 0, 1, 2 ecc.

Al secondo mese abbiamo le due coppie, ma la seconda non procreerà che dopo due mesi e così quest’ultima. Mentre le più vecchie lo faranno ogni mese. Contando i pinguini dalla prima coppia avremo sempre il numero ultimo della serie di Fibonacci a quella colonna, che è anche uguale al numero di coppie della colonna sommato alle coppie della colonna precedente.

Ma se, come ho detto questi numeri sono così interessanti vediamo di scoprire altro sulle loro caratteristiche e proprietà.

Proprietà della serie

Intanto è una successione infinita. E già potete immaginare, vedere con la vostra mente, la bellezza di qualcosa che è infinito. Già riuscire ad immaginarlo è uno sforzo intellettuale notevole. Però la sequenza non parte da zero, e questo semplifica le cose. Capirete che per un antico romano sarebbe stato difficile immaginare la serie. Anche solo ad una parte, perché se pensate alla notazione Romana dei numeri, si dovrebbero maneggiare alcuni numeri difficili da leggere o scrivere.

Ad esempio il quindicesimo numero in serie è il 987, che i Romani dovevano scrivere CMLXXXVII, il successivo è il 1.597 ovvero MDXCVII e poi c’è il 2.584, cioè il MMDLXXXIV, pensate ad un commerciante Romano, con l’abaco in mano, a calcolare il la somma degli ultimi due per ottenere il 4.181.

Leonardo (figlio di Guglielmo del, o dei, Bonacci) invece usava la notazione posizionale Araba/Indiana, con lo zero, ed il calcolo andava spedito fino a numeri altrimenti impensabili.

Ne riparleremo.

Parleremo anche di altro.

Giancarlo

Matematica,Natura,Senza categoria,Università

Successione di Fibonacci

Lascia un commento

La successione di Fibonacci.

Voglio affrontare un argomento di matematica che mi ha sempre appassionato: la successione di Fibonacci. E’ una serie di numeri particolare, scoperta studiando il comportamento animale, che può spiegare molti affascinanti aspetti della natura e le regole sottostanti.

L’ha scoperta un Pisano, Leonardo Pisano detto il Fibonacci, perché figlio di Guglielmo dei Bonacci nel tredicesimo secolo. Fibonacci era un commerciante che recatosi nel mondo arabo ne apprese e ne sviluppò nozioni matematiche allora sconosciute in Europa.

Successione di Fibonacci
Monument of Leonardo da Pisa (Fibonacci), by Giovanni Paganucci, completed in 1863, in the Camposanto di Pisa. Wikimedia

Ma qual’è questa successione e perché è così interessante?

1, 1, 2, 3, 5, 8, 13, 21, 34, 56, … all’infinito.

E’ interessante perché, a parte i primi due numeri gli altri si ottengono sommando i due precedenti. La serie è infinita. Una successione è una sequenza di numeri, successivi ovviamente, legati tra loro in modo particolare, per cui si può definirne il primo, il secondo, il terzo ed in generale l’ennesimo termine nello stesso modo generale. (Maggiori informazioni su wikipedia cliccando qui o in fondo all’articolo).

Perché il Fibonacci mi si piccò su questa successione?

Dicono che volesse conoscere quanti conigli si potessero avere da una coppia nel giro di un anno, forse lo voleva sapere perché amante dello stufato, forse per fornire la minima scorta iniziale alle navi dei commercianti Pisani, forse perché a Pisa nel tredicesimo secolo non avevano niente altro da fare, mah, chissà.

Fatto sta che scoprì questa successione e ne scrisse a proposito, ed eccoci qui a ricordarlo, come è giusto che sia per chi ha fatto qualcosa di grande.

La domanda che si pose Fibonacci, forse, era la seguente:

Se poniamo in un’area chiusa due conigli, che succede?

Beh prima di provare a rispondere chiariamo qualche regola altrimenti non andremo lontano, ed il percorso di questi numeri è lungo, anzi infinito.

I conigli nascono, nel primo mese crescono e nel secondo diventano sessualmente attivi e si accoppiano e si riproducono. Quindi procreano solo al secondo mese, poi lo fanno regolarmente ogni mese seguente. I conigli sono sempre accoppiati. Nascono e vivono in coppia. I conigli non muoiono mai. I conigli non mangiano, ne vengono mangiati.

In questo ideale mondo coniglio vediamo che succede.

Iniziamo il primo di gennaio 2014 con una bella coppia di conigli già adulti [1], dopo un mese il primo di Febbraio danno alla luce una nuova coppia di coniglietti [1,1]  il primo di Marzo la prima coppia mette al mondo una seconda coppia di coniglietti ed abbiamo due coppie di conigli fertili perché la seconda è cresciuta, ed una giovane [1,1,2] in un mese, il primo di Aprile, avremo la nascita di altre due coppie  mentre quelle mature saranno tre [1,1,2,3].

Passa un mese ed il primo Maggio, ancorché festa del lavoro, nasceranno tre nuove coppie e quelle sessualmente attive saranno cinque. [1,1,2,3,5]. Il primo Giugno anche queste tre nuove coppie si aggiungeranno alle cinque riproduttive mentre cinque nuove coppie nasceranno.[1,1,2,3,5,8]. A Luglio, passato metà anno, nasceranno otto nuove coppie da quelle mature e le cinque giovani passeranno la pubertà [1,1,2,3,5,8,13] Ad Agosto nasceranno ventun coppie e tredici saranno pronte per la sfida sessuale. [1,1,2,3,5,8,13,21]. A settembre saranno tanti. [1,1,2,3,5,8,13,21,34]. Ad Ottobre ancor di più. [1,1,2,3,5,8,13,21,34,55]. a Novembre si fatica a tener di conto. [1,1,2,3,5,8,13,21,34,55,89].

Eppoi, finalmente, a Dicembre si passa abbondantemente il centinaio di coppie di conigli fertili con quasi un centinaio di coniglietti al seguito. [1,1,2,3,5,8,13,21,34,55,89,144]. Ma l’anno non è finito ci manca un mese ed il primo Gennaio del 2015 avremo ottenuto dai nostri sforzi un mucchio di conigli saltellanti. [1,1,2,3,5,8,13,21,34,55,89,144,233]. Dove li metteremo!

Quindi ogni mese nasceranno

Quindi ogni mese nasceranno nuove coppie quante coppie sessualmente attive c’erano il mese precedente, mentre la popolazione in grado di riprodursi si accrescerà del numero di coppie giovani del mese prima.

Non è fantastica la progressione di questa serie di numeri? Pensate al secondo anno quanti conigli avremo (e sono tutte coppie), ed in un decennio? Saranno stati sufficienti per le mire del nostro caro Leonardo Pisano? Non lo sapremo mai, per intanto sappiamo qualcosa in più sulla matematica, sulle successioni eccetera.

Quindi, per concludere in qualche modo questa avventura: la successione Fibonacci sF(n), dati i due numeri iniziali sF(1) = 1 e sF(2) = 1, è generalizzabile per i numeri successivi come sF(n) = sF(n-1) + sF(n-2).

I numeri di questa successione sono ricorsivi.

Ma abbiamo visto solo l’inizio, siamo ancora al “carissimi amici”, ne riparleremo… se potremo, se vorremo, se…

Giancarlo