La congettura di Goldbach
La congettura di Goldbach non è stata ancora dimostrata, quindi non è mai diventata un teorema.
Goldbach stava studiando mezza matematica, nel senso che stava analizzando i numeri pari.
Non è cosa da poco, visto che sono sì la metà dei numeri naturali esistenti, ma sono pur sempre infiniti.
Verso la metà del diciottesimo secolo disse che tutti i numeri pari meno il primo (il due) si potevano scrivere (scomporre) come somma di due numeri primi, intendendo che il numero primo poteva anche essere ripetuto come nei primi due casi della lista che riporto qui sotto.
4=2+2
6=3+3
8=3+5
10=3+7
12=5+7
14=3+11
L’affermazione
è stata verificata negli anni per numeri sempre maggiori, fino ai giorni nostri in cui si è superato il traguardo dei duemila miliardi.
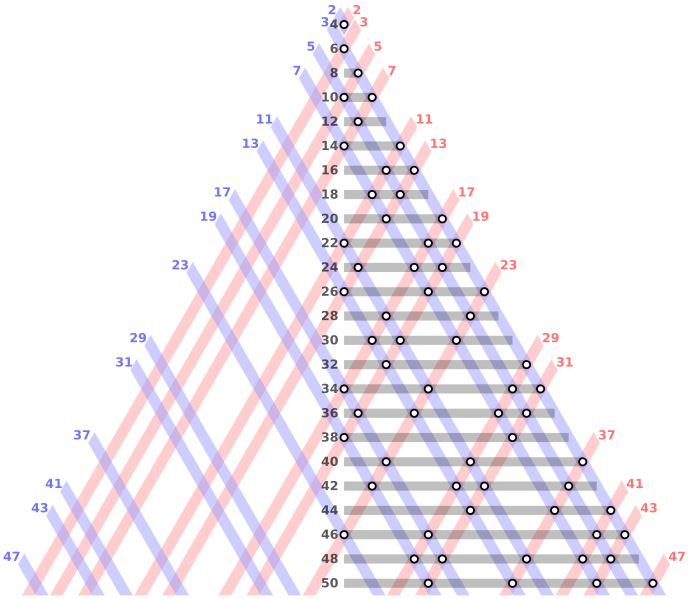
Tanti ci hanno provato, ma ancora senza successo, a dimostrare la verità della congettura.
Meriteresti un premio per la congettura di Goldbach
Se riuscissi a dimostrare la congettura meriteresti un premio. In effetti un premio a chi la risolve è stato già promesso e mai riscosso.
E’ stato offerto all’inizio di questo millennio, con la pubblicazione di un libro che si intitola “Lo zio Petros e la congettura di Goldbach”, romanzo scritto da Apostolos Doxiadis. E’ un racconto interessante in cui questo Petros, per non fare iscrivere suo nipote alla facoltà di matematica ed indirizzarlo verso studi migliori, gli propone di tentare la soluzione del problema.
Se riuscirà dimostrerà di essere ferrato in matematica e potrà seguire i suoi desideri, altrimenti accontenterà lo zio e si iscriverà a Diritto per diventare giudice o avvocato, o magari un politico. Naturalmente, nonostante gli sforzi di tutta un’estate il ragazzo non riuscirà nell’intento e si avvierà ad altri studi.
Ma il premio per la congettura di Goldbach?
Le case editrici del libro (Bloomsbury USA negli stati uniti e Faber and Faber in Gran Bretagna) offrirono, per lancio pubblicitario del volume, un milione di dollari a chi avesse dimostrato la congettura. Si doveva farlo prima dell’uscita del libro in libreria, due anni dopo.
Il libro ha avuto grande successo ma il premio è rimasto in tasca all’editore.
Giancarlo
Immagine base di copertina:
By Christian Goldbach – http://www.mscs.dal.ca/~joerg/pic/g-letter.jpg, Public Domain, https://commons.wikimedia.org/w/index.php?curid=1721422