Il sistema di numerazione Romano
Tra i tanti metodi di numerazione, il sistema di numerazione Romano merita qualche considerazione particolare.
Per prima cosa gli antichi Romani ce ne hanno lasciato ampia traccia nelle arti e nei mestieri, oltre che nella vita di tutti i giorni.
Naturalmente, come in tutti i sistemi, ci sono dei simboli che rappresentano i numeri, diversi da quelli che attualmente utilizziamo.
I simboli si sommano o si sottraggono a vicenda ed il numero rappresentato è il risultato di queste operazioni. Il sistema è quindi di tipo additivo/sottrattivo.
I simboli
Gli antichi Romani non avevano un simbolo per esprimere lo zero. Gli altri numeri espressi con un simbolo erano pochi:
I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000
Veramente pochi, sommando questi simboli non avrebbero potuto ottenere facilmente grandi numeri.
Sono dovuti ricorrere a trucchi.
Ad esempio, ponendo una linea sopra i simboli precedenti, ogni simbolo esprimeva un valore mille volte maggiore.
Centomila volte il valore si otteneva aggiungendo alla linea sopra, altre due linee ai bordi laterali del simbolo, mentre un milione di volte era espresso con una doppia linea sopra al simbolo numerico.
Come si enumera con questi simboli

Ogni numero è rappresentato da una stringa di simboli che rispetta le seguenti regole:
in ogni numero romano solo i simboli I, X, C e M possono essere ripetuti consecutivamente al massimo tre volte (a parte qualche numerazione Etrusca dove l’uno è ripetuto fino a quattro volte), mentre i simboli V, L e D possono essere inseriti solo una volta.
In una stringa di simboli senza valori crescenti il numero viene espresso sommando i valori dei simboli presenti: II = 2, III = 3, VI = 6, XIII = 13, CCXVI = 216, DCLVII = 657, ML = 1500.
Se invece un simbolo è seguito da un secondo di valore maggiore questo si deve sottrarre al successivo: IV = 4, IX = 9, XL = 40, XC = 90, CD = 400, CM = 900.
Naturalmente, per i numeri superiori al nove, i simboli successivi alla coppia sottrattiva devono avere valore inferiore.
Si possono sottrarre solo i simboli I, X e C.
Qualora un numero possa esprimersi con stringhe differenti si preferisce utilizzare quella più concisa, che è più facile da leggere e calcolare.
Numeri
La prima decina di numeri è:
I, II, II, IV, V, VI, VII, VIII, IX, X
Premettendo a questi il simbolo X si ottengono i successivi numeri da 11 a 20:
XI, XII, XII, XIV, XV, XVI, XVII, XVII, XIX, XX
Premettendo a questi un altro simbolo X si ottengono numeri da 21 a 30.
Ancora una X per ottenere dal 31 al 39, il quaranta non possiamo scriverlo con quattro X, quindi diviene XL.
Se a questo si fanno seguire i primi nove numeri della prima decina otteniamo da 41 a 49. Il cinquanta è L.
Naturalmente esistono anche le frazioni di numeri in numeri romani ma se volete potrete approfondirla da soli.
I calcoli con in numeri romani sono complessi e per questo si usava l’abaco.


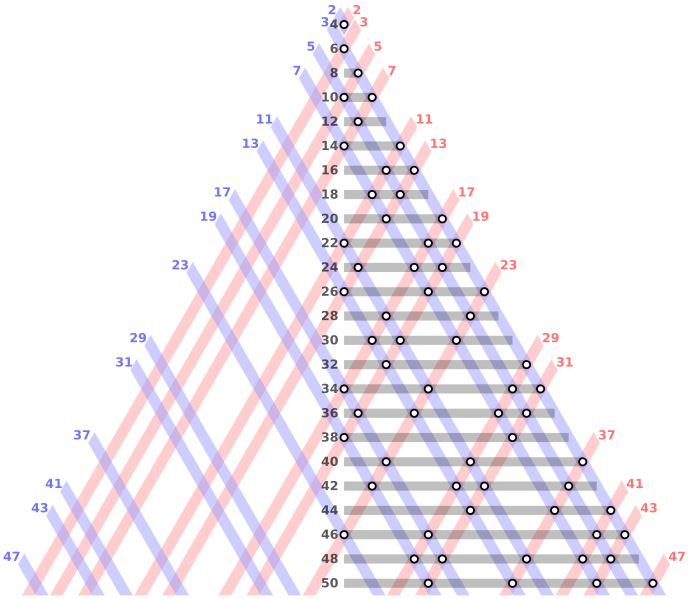













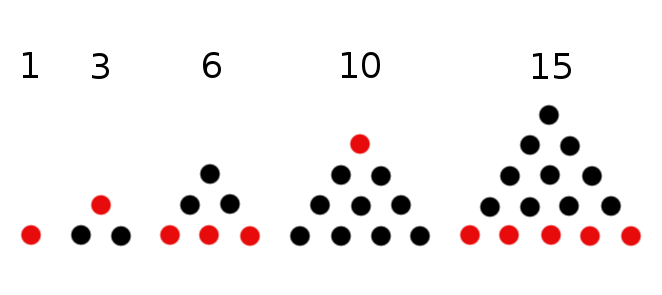

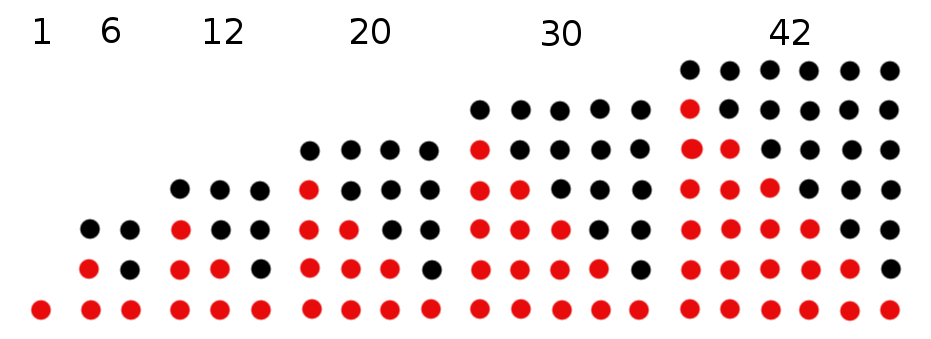
 ; questa proprietà fu scoperta da Gauss nel 1796, ed è un caso particolare del
; questa proprietà fu scoperta da Gauss nel 1796, ed è un caso particolare del  numeri triangolari è pari all’n-esimo
numeri triangolari è pari all’n-esimo  ; ogni altro numero triangolare è un
; ogni altro numero triangolare è un  Questo risultato è noto sotto il nome di
Questo risultato è noto sotto il nome di