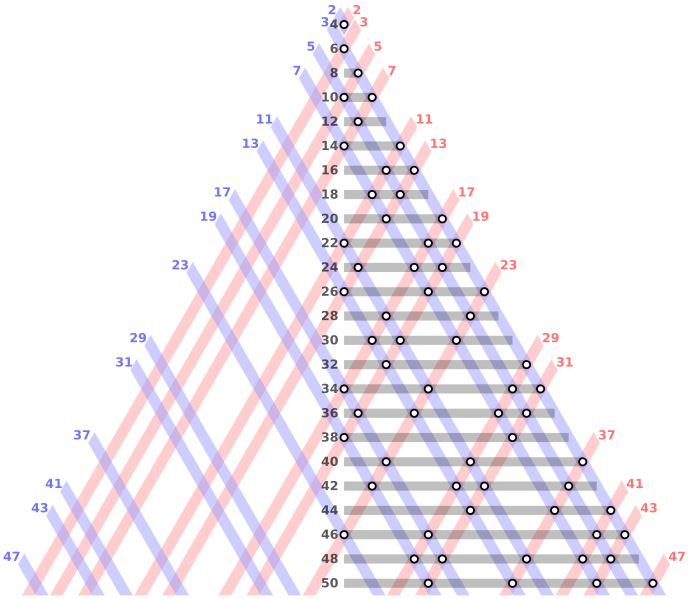
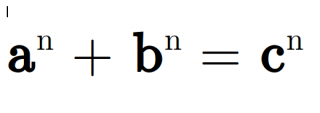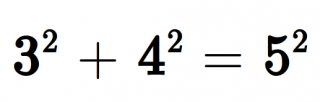Nascere poveri è brutto (*)
Gioiello, Joy come lo chiamavano gli amici, era nato povero, i suoi genitori erano contadini smessi, che nel ‘70 lasciarono il casolare per trasferirsi in paese, per trovare la felicità.
Contrariamente agli altri vicini, i suoi non avevano rubato niente al padrone della fattoria dove erano a mezzadria, ne gli rubarono qualcosa al momento di lasciare il podere, ne chiesero niente o fecero causa a lui o a chicchessia, come tanti a quel tempo.
Insomma da poveri contadini tristi divennero poveri operai, ma felici. Felici di poter garantire un avvenire al figlio.
Il padre che faceva il manovale in una ditta edile, la madre restò a casa ad accudire Gioiello. Allora non c’erano gli asili nido ne altre comodità odierne.
Comunque il babbo si ammazzò di lavoro per farlo crescere felice, che stesse meglio di lui, almeno.
Si ammazzò nel vero senso della parola quando, un giorno, cadde dal ponte che stava montando ed andò a battere la testa sulla betoniera, 7 o otto metri più sotto.
Gioiello di mamma
La mamma, disperata, superò a stento il dramma di quanto successo. Quando andò a servizio, la vita ricominciò a sorriderle. Riuscì anche a far studiare Joy, in modo che potesse trovar lavoro in banca ed essere felice.
Joy studiò sodo, voleva far contento la madre e poi voleva emergere, voleva lasciare quella condizione economica precaria.
Fu felice quando entrò in Banca, come cassiere, i soldi cominciarono ad arrivare e la miseria era ormai un ricordo.
Fu triste quando morì mamma ma la vita deve continuare come lo spettacolo.
Cominciò la sua carriera: tanti i cambi di ufficio, tanti quelli di mansione, tante automobili nel frattempo. Si sentì appagato e felice solo quando le fecero direttore generale, riuscendo a farsi una bella macchina, una casa grande in collina, una bella moglie giovane ed anche dei figli, che erano un amore: Belli ed intelligenti anche loro. Era finalmente felice, ricco e felice, non avrebbe desiderato altro, se non che anche i figli si sistemassero; in prospettiva, meglio di lui.
Ma un giorno, la mazzata. I figli erano stati arrestati per droga, non solo consumo ma anche spaccio. Droga pesante, di quella che si inietta.
Quando riuscì ad incontrarlo chiese al figlio maschio perché? E lui facendo spallucce “Oh babbo, per noia”.
Joy, Ohi.
A Joy crollò il mondo, sentì che nonostante tutti i soldi che aveva, e che aveva dato alla famiglia, che non aveva reso felice nessuno, nemmeno se stesso. Nepure conosceva i suoi figli, sua moglie, non aveva amici se non quelli interessati agli affari o che interessavano a lui per i suoi affari.
Non conosceva nessuno, veramente.
Non era nessuno, realmente.
Non era felice come non lo era nessuno intorno a lui, con lui.
Giancarlo
(*) Racconto basato sul paradosso di Easterlin.